ViT记录

NLP中seq2seq结构对self attention机制的引入

序列转序列结构常用于机器翻译，其分为编码器和解码器两部分。其中，编码器负责将输入文本转译为上下文编码向量，解码器负责对其进行解码，翻译为目标语言。

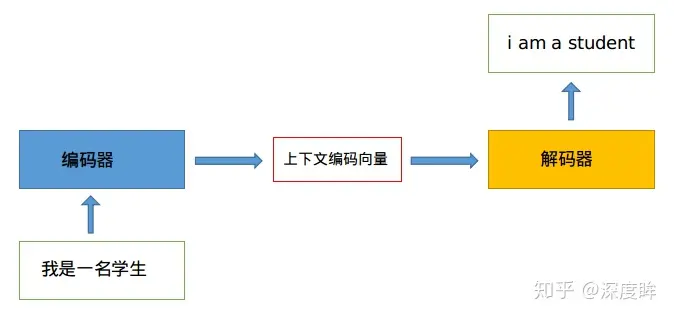
该上下文编码向量长度一般是固定的，导致模型对于变长输入文本的处理能力不一致。为了提升模型对于该序列的利用能力，学界引入了注意力机制根据输入序列的不同部分为其赋予不同的注意力权重。

对注意力机制进行抽象，可以归结为Q,K,V三个矩阵的计算，如下图所示：

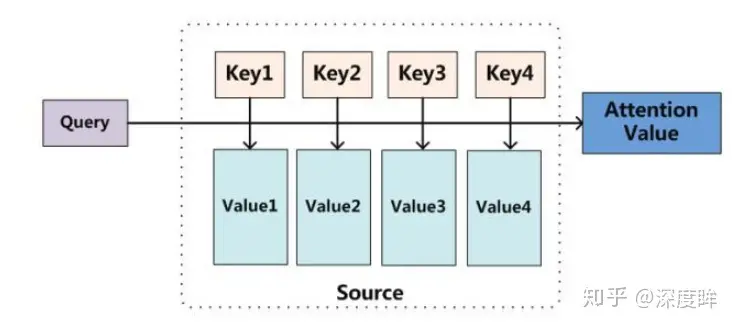
一个注意力层会在内部维护q,k,v三个权重矩阵，分别对应查询权重、键权重、值权重三方面权重。将输入序列向量与q,k,v矩阵分别相乘，就得到了Q（Query，查询向量，包含当前位置的输出序列信息，用于计算注意力权重）,K（Keys，键向量，包含序列中每个位置的信息，用于计算注意力权重）,V（Values，值向量，包含输入序列中每个位置的具体数值信息，用于根据注意力权重计算输出的上下文向量值）三个向量。

可以使用下面的公式表示从输入向量 x、待学习的 qkv 三个权重矩阵出发，得到注意力值的计算过程：

💡 1. 首先，对输入向量 x 进行线性变换得到查询（q）、键（k）和值（v）的向量表示。其中，\(W_q\)、 \(W_q\)和 \(W_q\)分别是待学习的查询、键和值的权重矩阵：

\[ q = W_q \cdot x \\ k = W_k \cdot x \\ v = W_v \cdot x \\ \]

1. 接下来，通过计算查询向量 q 和键向量 k 之间的相似度来计算注意力权重，其中，\(d_k\)是查询和键的向量维度：

\[ \text{Attention}(q, k) = \text{softmax}\left(\frac{q \cdot k^T}{\sqrt{d_k}}\right) \]

1. 最后，根据注意力权重对值向量 v 进行加权求和，得到注意力层输出的上下文向量：

\[ \text{Value} = \text{Attention}(q, k) \cdot v \]

对上述操作的理解：

• qkv三个矩阵的计算可以理解为使用对应权重对输入向量的线性变换

注意力机制的解释

从上述例子中我们可以知道，注意力机制的引入目的是“有的放矢”地处理中间向量，提高模型效率。其实在自注意力机制概念提出之前，已经有其他意义比较相近的研究被提出：

1. 自下而上的基于显著性的注意力机制：

   • maxpooling 最大池化
   • geating 门控

2. 自上而下的汇聚式注意力

   概念：从更高级别的表示或上下文信息开始，逐渐聚焦于更低级别的表示或局部信息

   💡 procedure:

   首先通过某种方式生成一个全局的上下文向量，通常是通过对整个输入序列做一次汇总或编码得到的。这个全局上下文向量可以被视为任务相关的高级表示，它包含了任务需要关注的重要信息。

   然后，针对输入序列中的每个元素，计算其与全局上下文向量之间的注意力权重。这些权重表示了每个元素对于全局上下文的重要性，即它们在给定任务中的相对重要程度。

   最后，根据计算得到的注意力权重，将各个元素的表示进行加权求和，得到最终的上下文表示。这个上下文表示综合了全局上下文和局部信息，可以用于后续的任务处理或决策。

   对于一个待加入注意力的输入序列\(X=(x_1,x_2,...,x_N)\)，其中N表示信息项数目，设\(z\in\{1,2,...,N\}\)表示被选择信息索引位置，给定一个和任务相关的查询（Query）向量q，则z=i的信息项的注意力值可以表示为：

   \[ p(z=i|X,q)=softmax(s(x_i,q)) \]

   其中\(s(x_i,q)\)为注意力打分函数，一般采用缩放点积形式来定义。注意这里面的d表示输入信息的维度。

   \[ s(x_i,q)=\frac{x_i^Tq}{\sqrt{d}} \]

   💡 用缩放点积形式定义注意力打分函数的原因

   1. 数值稳定性：缩放点积可以通过对点积结果进行缩放，将注意力分数限制在一个合适的范围内，避免了数值过大或过小的问题。通过缩放，可以使得注意力分数在相对较小的范围内，更利于数值计算的稳定性。
   2. 温度调节：缩放点积中的缩放因子通常称为温度参数（temperature parameter），可以调节注意力的分布形状。较高的温度会使得注意力更加平滑均匀，较低的温度会使得注意力更加集中和尖锐。温度参数的调节可以根据具体任务和需求来进行优化。