自注意力机制
Background
目的:从背景信息中挑选对当前任务目标更关键的信息。
应用场景:序列数据处理
机制分类:自注意力机制、空间注意力机制、时间注意力机制。
Classificiation
点积自注意力机制
NLP中自注意力机制的计算步骤:
预处理输入数据X
初始化权重\(W_Q,W_K,W_V\)
计算K,Q,V矩阵(仅限于输入部分的编码过程,encoder输出到decoder时的QKV不通过该方式计算)
\[ \begin{cases}K=XW_K\\Q=XW_Q\\V=XW_V\end{cases} \]
计算注意力得分:\(softmax(\frac{QK^T}{\sqrt{d_k}})\),然后再和V相乘
得到自注意力矩阵\(softmax(\frac{QK^T}{\sqrt{d_k}})V\)
其中,输入矩阵X通过乘以对应权重会生成对应的QKV矩阵,分别表征:
- Q:查询向量,代表需要关注的元素或者位置。
- K:键向量,代表参考元素或者位置。作用是用于提供参考信息,来确定序列中某一位置的元素相比于其他位置的元素的相关性。
- V:值向量,表示实际信息。输入向量X所在的空间不一定适用所有类型的任务的需要,比如一个数据在低秩空间可能是线性不可分的,但将其映射到高维空间后就可以找到一个明显的分界点。因此通过乘以一个可学习的权重矩阵\(W_V\),我们可以自适应的调节模型对输入向量的映射,从而提升模型对输入信息的学习能力。
然后,我们关注一下注意力得分的计算公式:
首先是Q和\(K^T\)的内积,这一项的意义在于度量Q和K两个向量的相似度。
考虑一组简单的二维向量:
1
2
3
4
5
6#固定的vector_a
vector_a = np.array([1, 0])
#夹角变化的vector_b,模长也是1,在单位圆上滑动
angle_degrees = [15, 45, 75, 105]
vector_b = np.array([np.cos(np.radians(angle)), np.sin(np.radians(angle))])我们编写如下脚本做一下可视化:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 创建一个模长固定的向量A
vector_a = np.array([1, 0])
# 创建一个包含不同夹角的列表
angle_degrees = [15, 45, 75, 105]
# 创建一个子图
fig, axes = plt.subplots(1, len(angle_degrees), figsize=(16, 4))
# 创建一个列表来存储内积值
dot_products = []
for i, angle in enumerate(angle_degrees):
# 计算向量B的坐标
vector_b = np.array([np.cos(np.radians(angle)), np.sin(np.radians(angle))])
# 计算内积
dot_product = np.dot(vector_a, vector_b)
dot_products.append(dot_product)
# 创建Seaborn风格的图形
sns.set()
# 绘制向量
axes[i].quiver(0, 0, vector_a[0], vector_a[1], angles='xy', scale_units='xy', scale=1, color='r', label='Vector A')
axes[i].quiver(0, 0, vector_b[0], vector_b[1], angles='xy', scale_units='xy', scale=1, color='b', label=f'Vector B ({angle} degrees)')
# 设置坐标轴范围
axes[i].set_xlim(-1.2, 1.2)
axes[i].set_ylim(-1.2, 1.2)
# 添加标签
axes[i].set_xlabel('X-axis')
axes[i].set_ylabel('Y-axis')
# 显示夹角和内积值
axes[i].text(-0.5, -0.2, f'Angle: {angle} degrees', ha='left')
axes[i].text(-0.5, -0.4, f'Dot Product: {dot_product:.2f}', ha='left')
# 添加网格
axes[i].grid(True)
axes[i].legend(loc='lower left')
# 设置子图之间的间隔
plt.tight_layout()
plt.savefig('/data/mmdSTTL/文档/compare.jpg')有如下的对比:
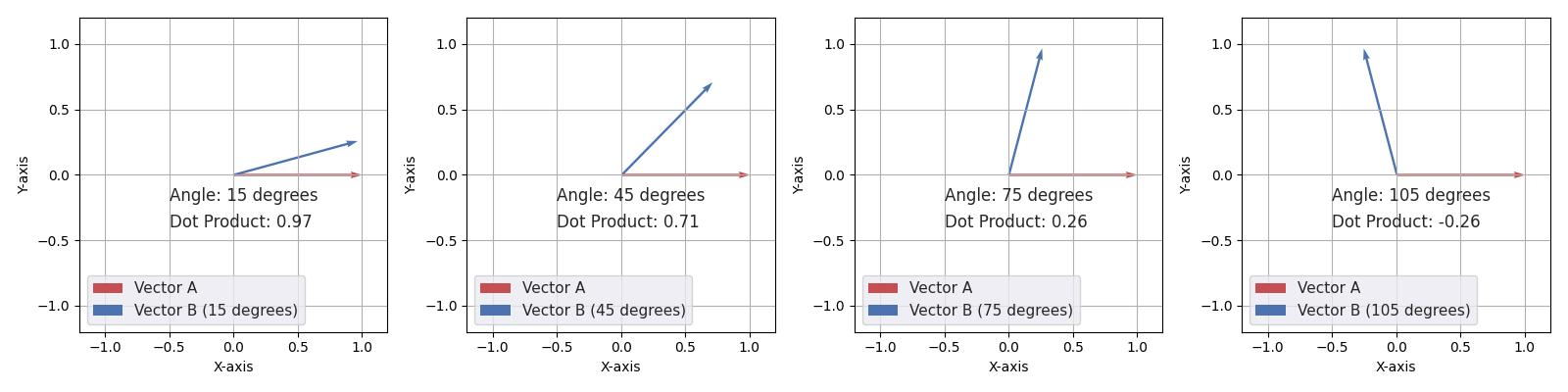
可见随着夹角从锐角向钝角变化,两个向量的内积值越来越小。因此我们可以认为两个向量内积值越大,它们之间的相似程度越高。因此可以用向量之间的内积值度量其相似性。
另外,由于Q和K都是来自于输入X的变换,而向量X可能不一定是方阵,所以必须得让K转置一下才能让两个向量求内积。所以体现到注意力公式里面就是\(QK^T\)。
然后是后续处理过程。我们通过除以对内积值做了一次重整,即\(\frac{QK^T}{\sqrt{d_k}}\)。这样做的意义在于缩放方差,使得方差较大的内积矩阵在softmax后尽量平滑。我们也可以通过如下脚本做一下可视化:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57import numpy as np
import matplotlib.pyplot as plt
# 创建一个复杂的输入矩阵
x = np.array([[1, 5, 3, 8],
[2, 7, 4, 9],
[6, 2, 7, 3],
[5, 3, 1, 6]])
# 定义未除以sqrt(d_k)的softmax函数
def softmax(x):
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum(axis=0, keepdims=True)
# 定义除以sqrt(d_k)的softmax函数
def scaled_softmax(x, sqrt_dk):
e_x = np.exp(x * sqrt_dk - np.max(x))
return e_x / e_x.sum(axis=0, keepdims=True)
# 假设 d_k = 4
sqrt_dk = 1.0 / np.sqrt(4)
# 计算未除以sqrt(d_k)和除以sqrt(d_k)后的softmax输出
softmax_output = softmax(x)
scaled_softmax_output = scaled_softmax(x, sqrt_dk)
# 创建热图来比较两者
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
# 绘制未除以sqrt(d_k)的softmax输出
cax1 = axes[0].matshow(softmax_output, cmap='viridis', aspect='auto')
plt.colorbar(cax1, ax=axes[0])
# 在每个格子中标注数字
for i in range(x.shape[0]):
for j in range(x.shape[1]):
axes[0].text(j, i, f'{softmax_output[i, j]:.2f}', ha='center', va='center', color='w')
axes[0].set_title('Softmax (Unscaled)')
axes[0].xaxis.set_ticks_position('top')
axes[0].xaxis.set_label_position('top')
# 绘制除以sqrt(d_k)后的softmax输出
cax2 = axes[1].matshow(scaled_softmax_output, cmap='viridis', aspect='auto')
plt.colorbar(cax2, ax=axes[1])
# 在每个格子中标注数字
for i in range(x.shape[0]):
for j in range(x.shape[1]):
axes[1].text(j, i, f'{scaled_softmax_output[i, j]:.2f}', ha='center', va='center', color='w')
axes[1].set_title('Scaled Softmax')
axes[1].xaxis.set_ticks_position('top')
axes[1].xaxis.set_label_position('top')
plt.tight_layout()
plt.savefig('/data/mmdSTTL/文档/compare.jpg')上述脚本的输出结果如下:
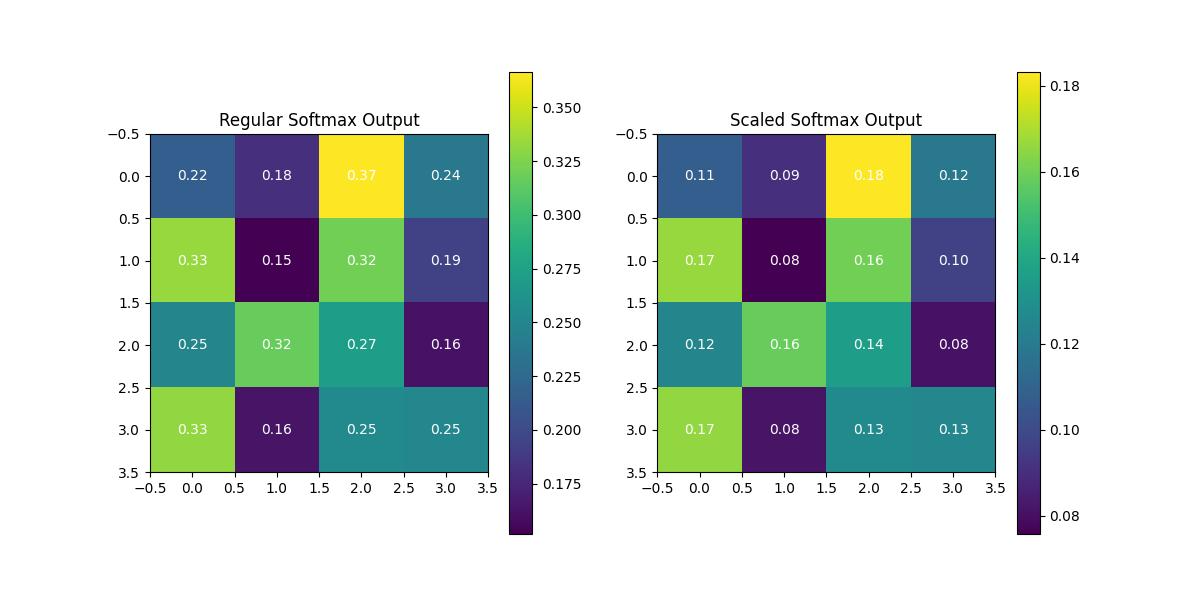
Terminal output:
Regular Softmax Output Variance: 0.004457626216288582 Scaled Softmax Output Variance: 0.0011144065540721454
可以看到,在scale(该例子中\(d_k=4\),即维度为4*4)后,softmax的输出矩阵方差变得更小,输出结果更加平滑。
至于softmax本身,老生常谈了,他的作用就是使得分布拉伸到总和为1的区间,使得输出值具有概率分布特征,可以用于度量相关性。对矩阵的softmax操作可以简单的表示为:
\[ \text{Softmax}(X)_{ij} = \frac{e^{x_{ij}}}{\sum_{k} e^{x_{ik}}} \]
我们对一个输入的一位序列做一下softmax并校验其性质:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# 生成一个随机的一维序列
sequence = np.random.rand(10)
# 计算 softmax
def softmax(x):
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum()
# 使用 softmax 进行平滑
smoothed_sequence = softmax(sequence)
# 创建数据框用于Seaborn绘图
import pandas as pd
data = pd.DataFrame({'Index': range(len(sequence)), 'Original Value': sequence, 'Smoothed Value': smoothed_sequence})
# 使用Seaborn绘制散点图,并连接同一个序列中的点
plt.figure(figsize=(10, 6))
plt.title("Connected Scatter Plot of Original and Smoothed Sequence")
plt.xlabel("Index")
plt.ylabel("Value")
# 绘制原始序列的点并添加标签
sns.lineplot(data=data, x='Index', y='Original Value', label=f"Original Sequence: sum={sequence.sum()}", color='b', marker="o")
# 绘制平滑后的序列的点并添加标签
sns.lineplot(data=data, x='Index', y='Smoothed Value', label=f"Smoothed Sequence: sum={smoothed_sequence.sum()}", color='r', marker="o")
# 添加图例
plt.legend()
plt.savefig('/data/mmdSTTL/文档/softmax.jpg')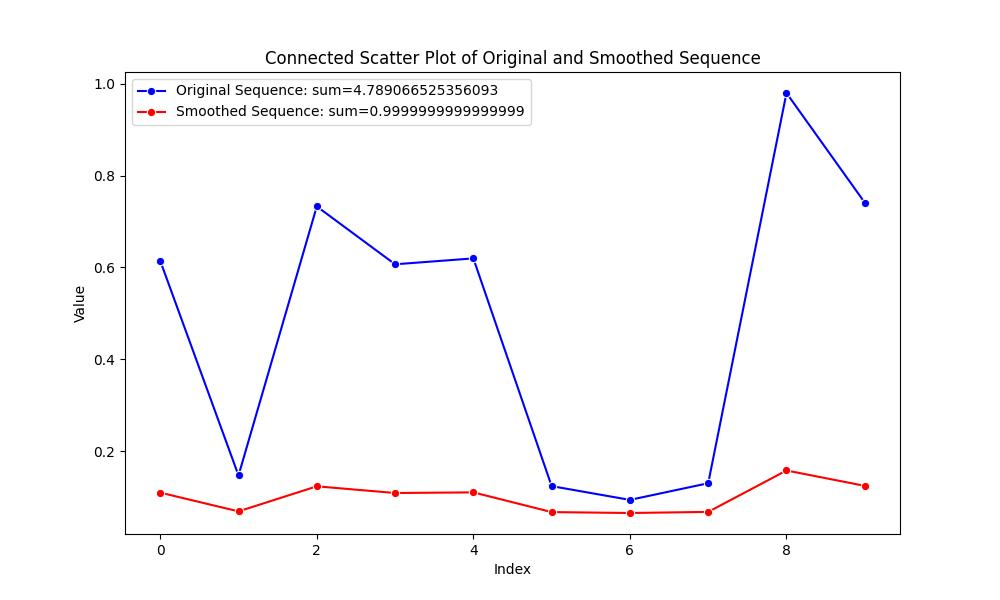
比如我们看上面这张图里面,softmax 函数将输入的元素转化为一个概率分布,使得序列的每个元素都在 0 到 1 的范围内,并且所有元素的和等于 1。
最后我们将结果乘上值矩阵V,就等于我们拿着算出来的权重给被查询的转换后的分布赋了一次权。因为\(QK^T\)是\((m,n)\times(n,m)=(m,m)\),所以可以直接乘上规模为\((m,n)\)的矩阵\(V\)。
加性注意力机制
带参数注意力计算
How Attention Mechanisms works in Decoder and Encoder
记注意力层的输入头分别为q,k,v,则:
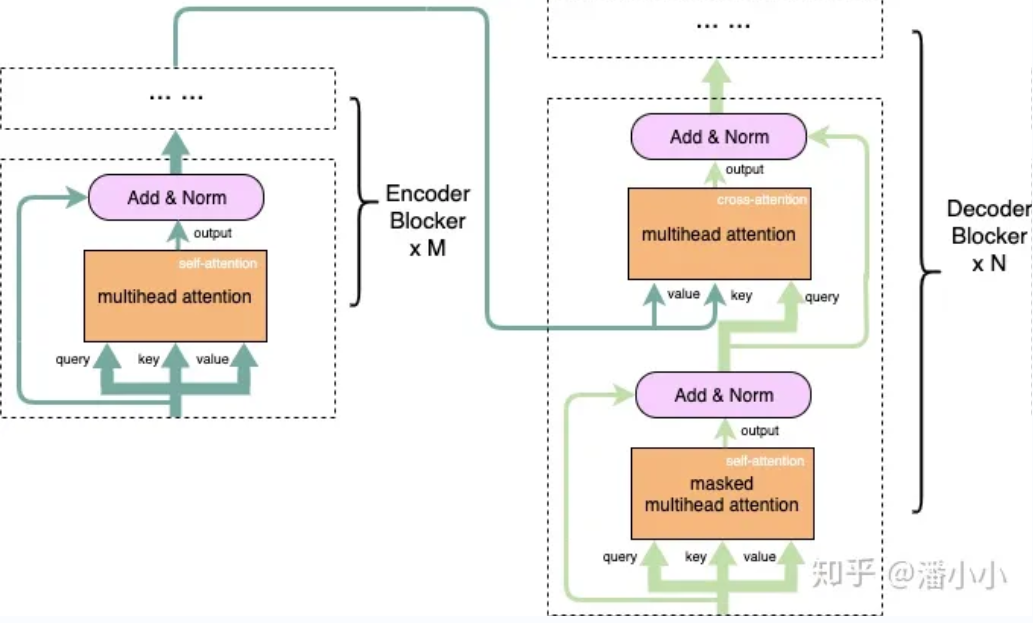
Encoder:只涉及自注意力机制,q,k,v都来自于上一层输出。即Encoder只会计算序列内部的相关性。
Decoder:涉及交叉注意力,q是来自于上一层输出的,但是kv两者都来自于一个encoder的输出。
decoder中的cross-attention的query对应了目标端序列,key, value对应了源端序列;
注意,第一个Decoder的输入是右移后(因为开始的时候,decoder的输入是一个特殊的起始符)的本模型上一次的预测结果;另外,decoder中的自注意力机制是masked的。这里分别进行解释:
mask:用于掩盖未来信息,避免模型在训练时过度依赖这些不应该被用来生成信息的数据。
We also modify the self-attention sub-layer in the decoder stack to prevent from attending to subsequent positions. This masking, combined with the fact that the output embeddings are offset by one position, ensures that the predictions for position i can depend only on the known outputs at positions less than i.
解释:在推理timestep=T的token时,decoder只能“看到”timestep < T的 T-1 个Token, 不能和timestep大于它自身的token做attention(因为根本还不知道后面的token是什么)。为了保证训练时和推理时的一致性,所以,训练时要同样防止token与它之后的token去做attention。
实现:在Decoder做self attention时,初始化一个下三角矩阵为0,上三角元素均为负无穷的矩阵加到注意力矩阵(这里指的是自注意机制中,点积或者加性注意力算出来的那个注意力矩阵)上。
第一个Decoder的输入是右移后的本模型上一次的预测结果
输入来源:
- Special
Token:通常,解码器在处理第一个时间步的输入时,会提供一个特殊的开始标记(如
</S>,表示"开始"),作为初始的输入。这个特殊标记告诉解码器开始生成目标端序列。 - 目标端序列:此外,解码器还接收整个目标端序列作为输入,尽管它在初始时不会使用整个序列。这是为了帮助模型学习如何在生成过程中依赖于目标序列的上下文信息。在初始时间步,解码器只会使用"Special Token"和自注意力机制来生成第一个目标词。
右移:开始的时候,decoder的输入是一个起始符。因此在循环地给decoder喂数据的时候,输入序列是右移一位了的输入序列。所以第一个Decoder的输入是右移后的本模型上一次的预测结果。
具体流程可以参照以下图片:

一个transformer翻译器的例子
- Special
Token:通常,解码器在处理第一个时间步的输入时,会提供一个特殊的开始标记(如
Multi-head Attention: heading higher data dimensions
多头注意力机制能够在不改变参数量的情况下增强每一层attention对输入序列的表示能力。
参考以下代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58class MultiHeadAttention(nn.Module):
def __init__(self, d_model, n_head):
super(MultiHeadAttention, self).__init__()
self.n_head = n_head
self.attention = ScaleDotProductAttention()
self.w_q = nn.Linear(d_model, d_model)
self.w_k = nn.Linear(d_model, d_model)
self.w_v = nn.Linear(d_model, d_model)
self.w_concat = nn.Linear(d_model, d_model)
def forward(self, q, k, v, mask=None):
# 1. dot product with weight matrices
q, k, v = self.w_q(q), self.w_k(k), self.w_v(v)
# 2. split tensor by number of heads
q, k, v = self.split(q), self.split(k), self.split(v)
# 3. do scale dot product to compute similarity
out, attention = self.attention(q, k, v, mask=mask)
# 4. concat and pass to linear layer
out = self.concat(out)
out = self.w_concat(out)
# 5. visualize attention map
# TODO : we should implement visualization
return out
def split(self, tensor):
"""
split tensor by number of head
:param tensor: [batch_size, length, d_model]
:return: [batch_size, head, length, d_tensor]
"""
batch_size, length, d_model = tensor.size()
d_tensor = d_model // self.n_head
tensor = tensor.view(batch_size, length, self.n_head, d_tensor).transpose(1, 2)
# it is similar with group convolution (split by number of heads)
return tensor
def concat(self, tensor):
"""
inverse function of self.split(tensor : torch.Tensor)
:param tensor: [batch_size, head, length, d_tensor]
:return: [batch_size, length, d_model]
"""
batch_size, head, length, d_tensor = tensor.size()
d_model = head * d_tensor
tensor = tensor.transpose(1, 2).contiguous().view(batch_size, length, d_model)
return tensor多头注意力的计算过程大概可以理解为将输入序列拆分成多个子序列,再对每个子序列分别计算注意力矩阵,然后再拼接结果。
- MHA接受两个参数:
- d_model:隐藏状态维度/嵌入维度。这一般指的是一个 token 通过嵌入层(embedding layer)计算得出的高维表示。
- n_head:注意力头数。这指的是需要将输入序列拆分成几个子序列;我们随后会调用split方法对qkv三个向量都进行拆分再进行注意力计算。
- MHA接受的向量输入规格为[batch_size, seq_length,
d_model],其意义为:
- batch_size:批次内数据量
- seq_length:输入序列的长度,即序列内token数
- d_model:嵌入维度,即一个token映射得到的高维表示
对于MHA内部实现的拆分和合并机制,可以做以下理解:我们把一个高维特征平均拆分成n_head份,然后对拆分后的各个qkv分别计算注意力矩阵,再分别乘上各自的值矩阵,最后再合并成完整的特征表示。
拆分部分的逻辑:直接将计算后得到的Q,K,V矩阵拆掉就行,后面直接使用这些子序列迭代进行计算。
1
2
3
4
5
6
7
8
9
10
11
12
13
14def split(self, tensor):
"""
split tensor by number of head
:param tensor: [batch_size, length, d_model]
:return: [batch_size, head, length, d_tensor]
"""
batch_size, length, d_model = tensor.size()
d_tensor = d_model // self.n_head
tensor = tensor.view(batch_size, length, self.n_head, d_tensor).transpose(1, 2)
# it is similar with group convolution (split by number of heads)
return tensor注意,在tensor那一行执行了两次形状调整:首先将tensor通过view方式改成(B,L,N,D),然后是将L,N交换,最后的输出维度是(batch_size, self.n_head, length, d_tensor),这样方便我们对拆出来的每个子矩阵做转置(\(Q_iK_i^T\)会用到);同时也符合ScaleDotProductAttention的输入格式。
缩放点积注意力计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33class ScaleDotProductAttention(nn.Module):
"""
compute scale dot product attention
Query : given sentence that we focused on (decoder)
Key : every sentence to check relationship with Qeury(encoder)
Value : every sentence same with Key (encoder)
"""
def __init__(self):
super(ScaleDotProductAttention, self).__init__()
self.softmax = nn.Softmax(dim=-1)
def forward(self, q, k, v, mask=None, e=1e-12):
# input is 4 dimension tensor
# [batch_size, head, length, d_tensor]
batch_size, head, length, d_tensor = k.size()
# 1. dot product Query with Key^T to compute similarity
k_t = k.transpose(2, 3) # transpose
score = (q @ k_t) / math.sqrt(d_tensor) # scaled dot product
# 2. apply masking (opt)
if mask is not None:
score = score.masked_fill(mask == 0, -10000)
# 3. pass them softmax to make [0, 1] range
score = self.softmax(score)
# 4. multiply with Value
v = score @ v
return v, score注意\(K_i^T\)是针对的拆出来的每个子序列,所以这里接受的输入是[B,H,L,D_T],然后transpose转的维度也是序号为2,3的两个维度。
注意这里的masking。输入的mask应该是一个只包含0和1,而且形状和该模块的形参中的qkv相同的张量。score是第一步点积计算出来的张量,原生支持.masked_fill方法。我们这里使用的是score.masked_fill(mask == 0, -10000),调用后会返回一个将score张量中满足mask==0的条件的位置替换成-10000的张量(-inf)。
合并部分的逻辑:
1
2
3
4
5
6
7
8
9
10
11
12def concat(self, tensor):
"""
inverse function of self.split(tensor : torch.Tensor)
:param tensor: [batch_size, head, length, d_tensor]
:return: [batch_size, length, d_model]
"""
batch_size, head, length, d_tensor = tensor.size()
d_model = head * d_tensor
tensor = tensor.transpose(1, 2).contiguous().view(batch_size, length, d_model)
return tensor合并的目的在于将以前分开的几个注意力头合并起来,得到新的特征矩阵。该部分涉及三个操作:
- 1,2维度转置,目的在于将张量形状调整回batch_size, length, head, d_tensor,方便后面合并。
- 调用.contiguous()方法将转置后的张量转变为连续存储。因为转置、veiw、切片等操作都可能会破坏张量在显存中存储的连续性,因此有必要在操作后调用contiguous方法保证其连续性。注意pytorch现在在大部分情况都会自动尝试保证张量连续性。
- 最后是view,把后两个维度合并到一起。这在逻辑上类似于把三段d_tensor首尾相连拼到一起。
- MHA接受两个参数: